|
| typedef Eigen::Matrix< double, OUT_DIM, 1 > | OUT_TYPE |
| | function output vector type More...
|
| |
| typedef Eigen::Matrix< double, OUT_DIM, IN_DIM > | JAC_TYPE |
| |
| typedef Eigen::Matrix< double, IN_DIM, IN_DIM > | HES_TYPE |
| |
| typedef std::function< OUT_TYPE(const IN_TYPE &)> | Function |
| | function tpye More...
|
| |
| typedef Eigen::Matrix< double, IN_DIM, 1 > | IN_TYPE |
| | function input vector type More...
|
| |
| typedef Eigen::Matrix< double, OUT_DIM, 1 > | OUT_TYPE |
| | function output vector type More...
|
| |
| typedef Eigen::Matrix< double, OUT_DIM, IN_DIM > | JAC_TYPE |
| |
| typedef Eigen::Matrix< double, IN_DIM, IN_DIM > | HES_TYPE |
| |
|
| | DerivativesNumDiff (Function &f, bool doubleSidedDerivative=false) |
| | default constructor More...
|
| |
| | DerivativesNumDiff (const DerivativesNumDiff &arg) |
| |
| virtual | ~DerivativesNumDiff () |
| | default destructor More...
|
| |
| DerivativesNumDiff * | clone () const override |
| | deep cloning More...
|
| |
| virtual OUT_TYPE | forwardZero (const Eigen::VectorXd &x) override |
| | Evaluates the method itself. More...
|
| |
| virtual JAC_TYPE | jacobian (const Eigen::VectorXd &x) override |
| | evaluate Derivatives at a given point More...
|
| |
| | Derivatives () |
| |
| virtual | ~Derivatives () |
| | default destructor More...
|
| |
| virtual void | sparseJacobian (const Eigen::VectorXd &x, Eigen::VectorXd &jac, Eigen::VectorXi &iRow, Eigen::VectorXi &jCol) |
| | Returns the evaluated jacobian in sparse format. More...
|
| |
| virtual Eigen::VectorXd | sparseJacobianValues (const Eigen::VectorXd &x) |
| | Returns the non zero values of the jacobian. More...
|
| |
| virtual HES_TYPE | hessian (const Eigen::VectorXd &x, const Eigen::VectorXd &lambda) |
| | Evaluates the hessian (2nd order derivatives with respect to input) of the method. In case of a vector valued function, the method returns the weighted sum of the hessians with weights w. More...
|
| |
| virtual void | sparseHessian (const Eigen::VectorXd &x, const Eigen::VectorXd &lambda, Eigen::VectorXd &hes, Eigen::VectorXi &iRow, Eigen::VectorXi &jCol) |
| | Returns the weighted sum of hessian of the problem in sparse format. More...
|
| |
| virtual Eigen::VectorXd | sparseHessianValues (const Eigen::VectorXd &x, const Eigen::VectorXd &lambda) |
| | Returns the non zero elements of the hessian of the problem. More...
|
| |
template<int IN_DIM, int OUT_DIM>
class ct::core::DerivativesNumDiff< IN_DIM, OUT_DIM >
Derivatives using Num-Diff Codegeneration.
Uses Num-Diff code generation to compute the Derivatives 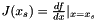 of a regular vector-valued mathematical function
of a regular vector-valued mathematical function 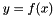 .
.
x has IN_DIM dimension and y has OUT_DIM dimension. Thus, they can be scalar functions (IN_DIM = 1, OUT_DIM = 1), fixed or variable size (IN_DIM = -1, OUT_DIM = -1) functions.
- Note
- In fact, this class is called Derivatives but computes also zero order derivatives
- Template Parameters
-
| IN_DIM | Input dimensionality of the function (use Eigen::Dynamic (-1) for dynamic size) |
| OUT_DIM | Output dimensionailty of the function (use Eigen::Dynamic (-1) for dynamic size) |



 Public Types inherited from ct::core::Derivatives< IN_DIM, OUT_DIM, double >
Public Types inherited from ct::core::Derivatives< IN_DIM, OUT_DIM, double > Public Member Functions inherited from ct::core::Derivatives< IN_DIM, OUT_DIM, double >
Public Member Functions inherited from ct::core::Derivatives< IN_DIM, OUT_DIM, double >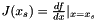 of a regular vector-valued mathematical function
of a regular vector-valued mathematical function 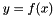 .
.