Often when working with a general nonlinear function 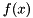 we are interested in its Jacobian (derivatives)
we are interested in its Jacobian (derivatives) 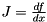 .
.
In order to compute this Jacobian, we are left with four methods
- Numerical differentiation, e.g.
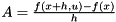
- Analytical, manually derivation
- Symbolic math engine
- Auto-Differentiation (with optional codegen)
The different methods are summarized below:
| Derivative Method | Numerical Accuracy | Computation Speed | Setup Time | Error Safe |
| Numeric Differentiation | - | - | +++ | +++ |
| Analytical Derivatives | +++ | ++ | - | - |
| Symbolic Math Engine | +++ | + | + | ++ |
| Automatic Differentiation | +++ | + | ++ | ++ |
| Auto-Diff Code Generation | +++ | +++ | ++ | ++ |
Bottom line: Automatic Differentiation is the tool of choice for accurate, yet easy to setup derivatives. For best performance, Automatic Differentiation with code generation (Auto-Diff Codgen) should be used. Auto-Diff Codegen is as accurate as analytical derivatives and equally fast if not faster!. For more on this please refer to the following publications: [3] [7]
- Note
- Both Auto-Diff and Auto-Diff Codegen require you to template your function on the scalar type. Please see the tutorial Templating your System or Function on the Scalar Type for tips and tricks on how to do this easily!
Jacobian/Derivative of a General Function
In this tutorial, we will compute the Jacobian (derivative) of a general function using Auto-Diff Codegeneration. For this let's look at the unit test found in ct_core/test/math/JacobianCGTest.h
#pragma once
const size_t inDim = 3;
const size_t outDim = 2;
const bool verbose = false;
typedef DerivativesCppadJIT<inDim, outDim> derivativesCppadJIT;
typedef DerivativesCppadCG<inDim, outDim> derivativesCppadCG;
typedef DerivativesCppad<inDim, outDim> derivativesCppad;
template <typename SCALAR>
Eigen::Matrix<SCALAR, outDim, 1>
testFunction(
const Eigen::Matrix<SCALAR, inDim, 1>& x)
{
Eigen::Matrix<SCALAR, outDim, 1> y;
y(0) = 3 * x(0) + 2 * x(0) * x(0) - x(1) * x(2);
y(1) = x(2) + x(1) + 3;
return y;
}
template <typename SCALAR>
Eigen::Matrix<SCALAR, outDim, inDim>
jacobianCheck(
const Eigen::Matrix<SCALAR, inDim, 1>& x)
{
Eigen::Matrix<SCALAR, outDim, inDim> jac;
jac << 3 + 4 * x(0), -x(2), -x(1), 0, 1, 1;
return jac;
}
template <typename SCALAR>
Eigen::Matrix<SCALAR, inDim, inDim>
hessianCheck(
const Eigen::Matrix<SCALAR, inDim, 1>& x,
const Eigen::Matrix<SCALAR, outDim, 1>& w)
{
Eigen::Matrix<SCALAR, inDim, inDim> hes;
hes << 4, 0, 0, 0, 0, -1, 0, -1, 0;
return w(0) * hes;
}
{
typename derivativesCppadJIT::FUN_TYPE_CG f_cg = testFunction<derivativesCppadJIT::CG_SCALAR>;
typename derivativesCppad::FUN_TYPE_AD f_ad = testFunction<derivativesCppad::AD_SCALAR>;
derivativesCppadJIT jacCG(f_cg);
derivativesCppad jacAd(f_ad);
DerivativesCppadSettings settings;
settings.createForwardZero_ = true;
settings.createJacobian_ = true;
settings.useDynamicLibrary_ = useDynamicLib;
Eigen::VectorXd someVec(inDim);
someVec.setRandom();
Eigen::VectorXd vecOut = jacAd.forwardZero(someVec);
jacCG.compileJIT(settings, "forwardZeroTestLib", verbose);
Eigen::VectorXd vecOut2 = jacCG.forwardZero(someVec);
ASSERT_LT((vecOut - vecOut2).array().abs().maxCoeff(), 1e-10);
}
{
typename derivativesCppadJIT::FUN_TYPE_CG f = testFunction<derivativesCppadJIT::CG_SCALAR>;
typename derivativesCppad::FUN_TYPE_AD f_ad = testFunction<derivativesCppad::AD_SCALAR>;
derivativesCppadJIT jacCG(f);
derivativesCppad jacAd(f_ad);
DerivativesCppadSettings settings;
settings.createJacobian_ = true;
settings.useDynamicLibrary_ = useDynamicLib;
jacCG.compileJIT(settings, "jacobianCGLib", verbose);
Eigen::Matrix<double, inDim, 1> x;
for (size_t i = 0; i < 1000; i++)
{
x.setRandom();
ASSERT_LT((jacCG.jacobian(x) -
jacobianCheck(x)).array().abs().maxCoeff(), 1e-10);
ASSERT_LT((jacAd.jacobian(x) -
jacobianCheck(x)).array().abs().maxCoeff(), 1e-10);
ASSERT_LT((jacCG.jacobian(x) - jacAd.jacobian(x)).array().abs().maxCoeff(), 1e-10);
}
}
{
typename derivativesCppadJIT::FUN_TYPE_CG f = testFunction<derivativesCppadJIT::CG_SCALAR>;
typename derivativesCppad::FUN_TYPE_AD f_ad = testFunction<derivativesCppad::AD_SCALAR>;
derivativesCppadJIT hessianCg(f);
derivativesCppad hessianAd(f_ad);
DerivativesCppadSettings settings;
settings.createHessian_ = true;
settings.useDynamicLibrary_ = useDynamicLib;
hessianCg.compileJIT(settings, "hessianCGLib", verbose);
Eigen::Matrix<double, inDim, 1> x;
Eigen::Matrix<double, outDim, 1> w;
for (size_t i = 0; i < 1000; ++i)
{
x.setRandom();
w.setRandom();
ASSERT_LT((hessianCg.hessian(x, w) -
hessianCheck(x, w)).array().abs().maxCoeff(), 1e-10);
ASSERT_LT((hessianAd.hessian(x, w) -
hessianCheck(x, w)).array().abs().maxCoeff(), 1e-10);
ASSERT_LT((hessianCg.hessian(x, w) - hessianAd.hessian(x, w)).array().abs().maxCoeff(), 1e-10);
}
}
{
typename derivativesCppadJIT::FUN_TYPE_CG f = testFunction<derivativesCppadJIT::CG_SCALAR>;
typename derivativesCppad::FUN_TYPE_AD f_ad = testFunction<derivativesCppad::AD_SCALAR>;
std::shared_ptr<derivativesCppadJIT> jacCG(new derivativesCppadJIT(f));
std::shared_ptr<derivativesCppad> jacAd(new derivativesCppad(f_ad));
DerivativesCppadSettings settings;
settings.createJacobian_ = true;
settings.useDynamicLibrary_ = useDynamicLib;
jacCG->compileJIT(settings, "jacobianCGLib", verbose);
Eigen::Matrix<double, inDim, 1> x;
std::shared_ptr<derivativesCppadJIT> jacCG_cloned(jacCG->clone());
if (useDynamicLib && (jacCG_cloned->getDynamicLib() == jacCG->getDynamicLib()))
{
std::cout << "FATAL ERROR: dynamic library not cloned correctly in JIT." << std::endl;
ASSERT_TRUE(false);
}
#ifdef LLVM
if (!useDynamicLib && (jacCG_cloned->getLlvmLib() == jacCG->getLlvmLib()))
{
std::cout << "FATAL ERROR: Llvm library not cloned correctly in JIT." << std::endl;
ASSERT_TRUE(false);
}
#endif
for (size_t i = 0; i < 100; i++)
{
x.setRandom();
ASSERT_LT((jacCG_cloned->jacobian(x) -
jacobianCheck(x)).array().abs().maxCoeff(), 1e-10);
ASSERT_LT((jacCG_cloned->jacobian(x) - jacAd->jacobian(x)).array().abs().maxCoeff(), 1e-10);
}
}
TEST(JacobianCGTest, ForwardZeroTest)
{
try
{
#ifdef LLVM
#endif
} catch (std::exception& e)
{
std::cout << "Exception thrown: " << e.what() << std::endl;
ASSERT_TRUE(false);
}
}
TEST(JacobianCGTest, JITCompilationTest)
{
try
{
#ifdef LLVM
#endif
} catch (std::exception& e)
{
std::cout << "Exception thrown: " << e.what() << std::endl;
ASSERT_TRUE(false);
}
}
TEST(HessianCGTest, JITHessianTest)
{
try
{
#ifdef LLVM
#endif
} catch (std::exception& e)
{
std::cout << "Exception thrown: " << e.what() << std::endl;
ASSERT_TRUE(false);
}
}
TEST(JacobianCGTest, DISABLED_LlvmCloneTest)
{
try
{
} catch (std::exception& e)
{
std::cout << "Exception thrown: " << e.what() << std::endl;
ASSERT_TRUE(false);
}
}
TEST(JacobianCGTest, JitCloneTest)
{
try
{
} catch (std::exception& e)
{
std::cout << "Exception thrown: " << e.what() << std::endl;
ASSERT_TRUE(false);
}
}
TEST(JacobianCGTest, CodegenTest)
{
typename derivativesCppadCG::FUN_TYPE_CG f = testFunction<derivativesCppadCG::CG_SCALAR>;
derivativesCppadCG jacCG(f);
jacCG.generateJacobianSource("TestJacobian");
jacCG.generateForwardZeroSource("TestForwardZero");
jacCG.generateHessianSource("TestHessian");
}
So what do we see here? In the first test, even though we do code generation, we can evaluate the Jacobian at runtime without recompiling our code. The code gets compiled in the background. This gives maximum speed while maintaining flexibility. For simple functions this process is very fast. However, what if our function is more complex? In this case, the second tests shows how to generate source code and actually write it to file.
But what is this ct::core::JacobianCG::generateForwardZeroCode()? Well it generates code for the original function. So in the end, it regenerates the function. But why is this even relavant? For such a simple example as here, there is probably not a lot of difference. However, for more complex equations, a regenerated function can be faster by up to 2x or more. The reason for that is that Auto-Diff builds an expression graph that can optimize the original function. Since it is case dependent whether you gain speed or not, you will have to try it out.
Jacobian/Linearization of a Nonlinear System
Often when dealing with nonlinear systems, described by a differential equation of the form 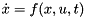 we wish to compute the linearized form of the system around an operating point
we wish to compute the linearized form of the system around an operating point 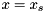 ,
, 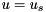 .
.
![\[ \dot{x} = A(x_s, u_s) x + B(x_s, u_s) u \]](form_7.png)
with the System's Jacobians with respect to state and input
![\[ \begin{aligned} A &= \frac{df}{dx} |_{x=x_s, u=u_s} \\ B &= \frac{df}{du} |_{x=x_s, u=u_s} \end{aligned} \]](form_8.png)
As in the example above, we are left with different methods for computing the Jacobians. In the Control Toolbox the following methods are implemented for linearizing a ct::core::System.
- Numerical Differentiation, see ct::core::SystemLinearizer
- Automatic Differentiation, see ct::core::AutoDiffLinearizer
- Auto-Diff Codegen, see ct::core::ADCodegenLinearizer
Again, the same properties as above hold in terms of speed, accuracy, setup time etc. As an example on how to use these different classes, let's again look at a unit test, this time at ct_core/test/math/AutoDiffLinearizerTest.cpp. This unit test shows how to use numerical and automatic differentiation to compute the linearization.
#include <gtest/gtest.h>
using std::shared_ptr;
TEST(AutoDiffLinearizerTest, SystemLinearizerComparison)
{
typedef CppAD::AD<double> AD_Scalar;
typedef Eigen::Matrix<double, state_dim, state_dim> A_type;
typedef Eigen::Matrix<double, state_dim, control_dim> B_type;
double w_n = 100;
AutoDiffLinearizer<state_dim, control_dim> adLinearizer(nonlinearSystemAD);
std::shared_ptr<AutoDiffLinearizer<state_dim, control_dim>> adLinearizerClone(adLinearizer.clone());
double t = 0;
for (size_t i = 0; i < 1000; i++)
{
x.setRandom();
u.setRandom();
A_type A_system = systemLinearizer.getDerivativeState(x, u, t);
B_type B_system = systemLinearizer.getDerivativeControl(x, u, t);
A_type A_ad = adLinearizer.getDerivativeState(x, u, t);
B_type B_ad = adLinearizer.getDerivativeControl(x, u, t);
A_type A_adCloned = adLinearizerClone->getDerivativeState(x, u, t);
B_type B_adCloned = adLinearizerClone->getDerivativeControl(x, u, t);
ASSERT_LT((A_system - A_ad).array().abs().maxCoeff(), 1e-5);
ASSERT_LT((B_system - B_ad).array().abs().maxCoeff(), 1e-5);
ASSERT_LT((A_system - A_adCloned).array().abs().maxCoeff(), 1e-5);
ASSERT_LT((B_system - B_adCloned).array().abs().maxCoeff(), 1e-5);
}
}
TEST(AutoDiffDiscreteLinearizerTest, DiscreteSystemLinearizerComparison)
{
typedef CppAD::AD<double> AD_Scalar;
const double rate = 0.1;
shared_ptr<TestDiscreteNonlinearSystemAD> nonlinearSystemAD(
DiscreteSystemLinearizerAD<state_dim, control_dim> adLinearizer(nonlinearSystemAD);
std::shared_ptr<DiscreteSystemLinearizerAD<state_dim, control_dim>> adLinearizerClone(adLinearizer.clone());
int n = 0;
for (size_t i = 0; i < 1000; i++)
{
x.setRandom();
u.setRandom();
A_type A_system = systemLinearizer.getDerivativeState(x, u, n);
B_type B_system = systemLinearizer.getDerivativeControl(x, u, n);
A_type A_system2;
B_type B_system2;
systemLinearizer.getAandB(x, u, x, n, 1, A_system2, B_system2);
ASSERT_LT((A_system - A_system2).array().abs().maxCoeff(), 1e-5);
ASSERT_LT((B_system - B_system2).array().abs().maxCoeff(), 1e-5);
A_type A_system_analytic;
A_system_analytic << 1.0 + rate * u(0), 0.0, x(1) * x(1), 2.0 * x(0) * x(1);
B_type B_system_analytic;
B_system_analytic << rate * x(0), 0.0;
ASSERT_LT((A_system - A_system_analytic).array().abs().maxCoeff(), 1e-5);
ASSERT_LT((B_system - B_system_analytic).array().abs().maxCoeff(), 1e-5);
A_type A_ad = adLinearizer.getDerivativeState(x, u, n);
B_type B_ad = adLinearizer.getDerivativeControl(x, u, n);
A_type A_adCloned = adLinearizerClone->getDerivativeState(x, u, n);
B_type B_adCloned = adLinearizerClone->getDerivativeControl(x, u, n);
ASSERT_LT((A_system - A_ad).array().abs().maxCoeff(), 1e-5);
ASSERT_LT((B_system - B_ad).array().abs().maxCoeff(), 1e-5);
ASSERT_LT((A_system - A_adCloned).array().abs().maxCoeff(), 1e-5);
ASSERT_LT((B_system - B_adCloned).array().abs().maxCoeff(), 1e-5);
}
}
TEST(AutoDiffLinearizerTestMP, SystemLinearizerComparisonMP)
{
typedef std::shared_ptr<AutoDiffLinearizer<state_dim, control_dim>> AdLinearizerPtr;
typedef CppAD::AD<double> AD_Scalar;
typedef Eigen::Matrix<double, state_dim, state_dim> A_type;
typedef Eigen::Matrix<double, state_dim, control_dim> B_type;
double w_n = 100;
AutoDiffLinearizer<state_dim, control_dim> adLinearizer(nonlinearSystemAD);
std::vector<std::shared_ptr<SystemLinearizer<state_dim, control_dim>>> systemLinearizers;
size_t runs = 1000;
size_t numThreads = 5;
for (size_t i = 0; i < numThreads; ++i)
systemLinearizers.push_back(
CppadParallel::initParallel(numThreads + 1);
for (size_t n = 0; n < runs; ++n)
{
std::vector<std::thread> threads;
for (size_t i = 0; i < numThreads; ++i)
{
threads.push_back(std::thread([i, state_dim, control_dim, &adLinearizer, &systemLinearizers]() {
AdLinearizerPtr adLinearizerLocal = AdLinearizerPtr(adLinearizer.clone());
StateVector x;
ControlVector u;
double t = 0.0;
x.setRandom();
u.setRandom();
A_type A_system = systemLinearizers[i]->getDerivativeState(x, u, t);
B_type B_system = systemLinearizers[i]->getDerivativeControl(x, u, t);
A_type A_ad = adLinearizerLocal->getDerivativeState(x, u, t);
B_type B_ad = adLinearizerLocal->getDerivativeControl(x, u, t);
ASSERT_LT((A_system - A_ad).array().abs().maxCoeff(), 1e-5);
ASSERT_LT((B_system - B_ad).array().abs().maxCoeff(), 1e-5);
}));
}
for (auto& thr : threads)
thr.join();
}
CppadParallel::resetParallel();
}
int main(
int argc,
char** argv)
{
testing::InitGoogleTest(&argc, argv);
return RUN_ALL_TESTS();
}
For an example on how to use Auto-Diff Codegen to compute the linearization, see ADCodegenLinearizerTest.h
- Note
- Both Auto-Diff and Auto-Diff Codegen require you to template your function on the scalar type. Please see the tutorial Templating your System or Function on the Scalar Type for tips and tricks on how to do this easily!
Templating your System or Function on the Scalar Type
In order to make use of Auto-Differentiation, you need to template your system on the scalar type. This means Auto-Diff needs to be able to call your system function with a special type, rather than a regular float or double type. If your modelling framework does not support this natively (as often the case), here is a short guide on how to add Auto-Diff support. Luckily, the Eigen library already templates its type on the scalar type already. Thus, if you are using Eigen, this process is even easier.
There are different ways of templating your code on the scalar type. Here, we describe one of several options. Assume you have your class that contains your model/system:
namespace my_sys {
class MySystem :
public ct:core::ControlledSystem<2, 1> {
public:
size_t STATE_DIM = 2;
size_t INPUT_DIM = 1;
const double& t,
const ControlVector<CONTROL_DIM>& control,
private:
double my_paramter_;
};
}
The first step is to template your class on the scalar type. When doing so, we recommend moving your class to a new subnamespace (here called "tpl"). The reason to do so is that you can add a "using" directive in the original namespace, that defines your class with its original scalar type. In this way, all other code you might have written is not affected and continues to work. As a second step, you replace all double or floats or whatever scalar type you used before with the template parameter. CT types are already templated on scalar types, making your life much easier. The result would look something like this:
namespace my_sys {
namespace tpl {
template <typename SCALAR>
public:
size_t STATE_DIM = 2;
size_t INPUT_DIM = 1;
void computeControlledDynamics(const StateVector<STATE_DIM, SCALAR>& state,
const ControlVector<CONTROL_DIM, SCALAR>& control,
StateVector<STATE_DIM, SCALAR>& derivative) override;
private:
};
}
using MySystem = tpl::MySystem<double>;
}
- Note
- Fixed quantities such as the state dimension obviously do not need to be type converted.
-
It is not strictly necessary to change the parameter ("my_parameter_") to SCALAR type as well. However, you can then use Auto-Diff to derive e.g. your dynamics function by this parameter if you ever wanted to do parametric optimization or system identification. Cool eh? :)
-
Since your class is templated now, make sure you move the implementation from the .cpp file to the .h file (or an implementation file that gets included in the .h file).
-
In case your class is already templated (on anything really), one option is to add the scalar type to the list of templates and default it to whatever scalar type you used before.
There are some pitfalls when using Auto-Differentiation. Please read the notes below.
In order to make sure your class works with Auto-Differentiation, your code needs to comply with some restrictions: Ideally, your code should not contain branching, i.e. no if/else, switch or for loops that depend on an Auto-Diff scalar. While there are proper ways of dealing with branching you might not want to start out with it. Branching that depends only on paramters of which you do not want to take the derivative of is fine. Using mathematical functions or linear algebra: Functions such as std::sin, std::exp or inverses of Eigen matrices either do not support scalar types or have internal branching. Thus, they cannot be used. Thus, we provide traits that help you in this situation. These traits will select appropriate functions to call, depending on which SCALAR type is used. In case you called std::sin before, you should now call ct::core::tpl::TraitSelector<SCALAR>::Trait::sin. In case e.g. SCALAR is a double type, this will call std::sin but for instances of the Auto-Diff scalar it will call the Auto-Diff compatible versions of sin.
Once the conversion is completed, you can follow the instructions above to compute Jacobians.


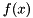 we are interested in its Jacobian (derivatives)
we are interested in its Jacobian (derivatives) 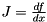 .
.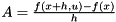
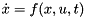 we wish to compute the linearized form of the system around an operating point
we wish to compute the linearized form of the system around an operating point 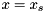 ,
, 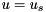 .
.![\[ \dot{x} = A(x_s, u_s) x + B(x_s, u_s) u \]](form_7.png)
![\[ \begin{aligned} A &= \frac{df}{dx} |_{x=x_s, u=u_s} \\ B &= \frac{df}{du} |_{x=x_s, u=u_s} \end{aligned} \]](form_8.png)