Computes the linearization of a system dynamics function through numerical finite differencing. More...

#include <DynamicsLinearizerNumDiff.h>

Public Types
typedef ControlVector< CONTROL_DIM, SCALAR >	control_vector_t
	control vector type More...

typedef StateMatrix< STATE_DIM, SCALAR >	state_matrix_t
	state Jacobian type (A) More...

typedef StateControlMatrix< STATE_DIM, CONTROL_DIM, SCALAR >	state_control_matrix_t
	control Jacobian type (B) More...

typedef std::function< void(const state_vector_t &, const TIME &, const control_vector_t &, state_vector_t &)>	dynamics_fct_t
	dynamics function signature More...

Public Member Functions
	DynamicsLinearizerNumDiff (dynamics_fct_t dyn, bool doubleSidedDerivative=true)
	default constructor More...

	DynamicsLinearizerNumDiff (const DynamicsLinearizerNumDiff &rhs)
	copy constructor More...

const state_matrix_t &	getDerivativeState (const state_vector_t &x, const control_vector_t &u, const TIME t=TIME(0))
	get the Jacobian with respect to the state More...

const state_control_matrix_t &	getDerivativeControl (const state_vector_t &x, const control_vector_t &u, const TIME t=TIME(0))
	get the Jacobian with respect to the input More...

bool	getDoubleSidedDerivativeFlag () const

Public Attributes
EIGEN_MAKE_ALIGNED_OPERATOR_NEW typedef StateVector< STATE_DIM, SCALAR >	state_vector_t
	state vector type More...

Protected Attributes
dynamics_fct_t	dynamics_fct_
	function handle to system dynamics More...

bool	doubleSidedDerivative_
	flag if double sided numerical differentiation should be used More...

SCALAR	eps_
	perturbation for numerical differentiation More...

state_matrix_t	dFdx_
	Jacobian wrt state. More...

state_control_matrix_t	dFdu_
	Jacobian wrt input. More...

state_vector_t	res_ref_
	reference result for numerical differentiation More...

Detailed Description

template<size_t STATE_DIM, size_t CONTROL_DIM, typename SCALAR, typename TIME>
class ct::core::DynamicsLinearizerNumDiff< STATE_DIM, CONTROL_DIM, SCALAR, TIME >

Computes the linearization of a system dynamics function through numerical finite differencing.

This class takes a function handle representing system dynamics of the form 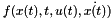$f(x(t),t,u(t),\dot{x(t)})$ or $ f(x[n],n,u[n],x[n+1]) $ where the last argument is the result of the evaluation in each case. It then computes the linearization around a given point $ x = x_s $ , $ u = u_s $ .

Finite differencing is used to calculate partial derivatives

$\begin{aligned} A &= \frac{df}{dx} |_{x=x_s, u=u_s} \\ B &= \frac{df}{du} |_{x=x_s, u=u_s} \end{aligned}$

Member Typedef Documentation

◆ control_vector_t

template<size_t STATE_DIM, size_t CONTROL_DIM, typename SCALAR, typename TIME>

typedef ControlVector<CONTROL_DIM, SCALAR> ct::core::DynamicsLinearizerNumDiff< STATE_DIM, CONTROL_DIM, SCALAR, TIME >::control_vector_t

control vector type

◆ state_matrix_t

template<size_t STATE_DIM, size_t CONTROL_DIM, typename SCALAR, typename TIME>

typedef StateMatrix<STATE_DIM, SCALAR> ct::core::DynamicsLinearizerNumDiff< STATE_DIM, CONTROL_DIM, SCALAR, TIME >::state_matrix_t

state Jacobian type (A)

◆ state_control_matrix_t

template<size_t STATE_DIM, size_t CONTROL_DIM, typename SCALAR, typename TIME>

typedef StateControlMatrix<STATE_DIM, CONTROL_DIM, SCALAR> ct::core::DynamicsLinearizerNumDiff< STATE_DIM, CONTROL_DIM, SCALAR, TIME >::state_control_matrix_t

control Jacobian type (B)

◆ dynamics_fct_t

template<size_t STATE_DIM, size_t CONTROL_DIM, typename SCALAR, typename TIME>

typedef std::function<void(const state_vector_t&, const TIME&, const control_vector_t&, state_vector_t&)> ct::core::DynamicsLinearizerNumDiff< STATE_DIM, CONTROL_DIM, SCALAR, TIME >::dynamics_fct_t

dynamics function signature

Constructor & Destructor Documentation

◆ DynamicsLinearizerNumDiff() [1/2]

template<size_t STATE_DIM, size_t CONTROL_DIM, typename SCALAR, typename TIME>

ct::core::DynamicsLinearizerNumDiff< STATE_DIM, CONTROL_DIM, SCALAR, TIME >::DynamicsLinearizerNumDiff	(	dynamics_fct_t	dyn,
		bool	doubleSidedDerivative = `true`
	)

inline

default constructor

Initializes the linearizer with a dynamics function object

Parameters

nonlinearSystem	non-linear system to linearize
doubleSidedDerivative	if true, double sided numerical differentiation is used

◆ DynamicsLinearizerNumDiff() [2/2]

template<size_t STATE_DIM, size_t CONTROL_DIM, typename SCALAR, typename TIME>

ct::core::DynamicsLinearizerNumDiff< STATE_DIM, CONTROL_DIM, SCALAR, TIME >::DynamicsLinearizerNumDiff ( const DynamicsLinearizerNumDiff< STATE_DIM, CONTROL_DIM, SCALAR, TIME > & rhs )

inline

copy constructor

Member Function Documentation

◆ getDerivativeState()

template<size_t STATE_DIM, size_t CONTROL_DIM, typename SCALAR, typename TIME>

const state_matrix_t& ct::core::DynamicsLinearizerNumDiff< STATE_DIM, CONTROL_DIM, SCALAR, TIME >::getDerivativeState	(	const state_vector_t &	x,
		const control_vector_t &	u,
		const TIME	t = `TIME(0)`
	)

inline

get the Jacobian with respect to the state

This computes the linearization of the dynamics with respect to the state at a given point $ x=x_s $ , $ u=u_s $ , i.e. it computes

$B = \frac{df}{dx} |_{x=x_s, u=u_s}$

Parameters

x	state to linearize at
u	control to linearize at
t	time

Returns: Jacobian wrt state

Referenced by ct::core::DiscreteSystemLinearizer< STATE_DIM, CONTROL_DIM, SCALAR >::getAandB(), ct::core::DiscreteSystemLinearizer< STATE_DIM, CONTROL_DIM, SCALAR >::getDerivativeState(), and ct::core::SystemLinearizer< STATE_DIM, CONTROL_DIM, SCALAR >::getDerivativeState().

◆ getDerivativeControl()

template<size_t STATE_DIM, size_t CONTROL_DIM, typename SCALAR, typename TIME>

const state_control_matrix_t& ct::core::DynamicsLinearizerNumDiff< STATE_DIM, CONTROL_DIM, SCALAR, TIME >::getDerivativeControl	(	const state_vector_t &	x,
		const control_vector_t &	u,
		const TIME	t = `TIME(0)`
	)